Tracing Intersection Curve Segment:
After having estimated the starting point of an intersection curve
segment, we need to integrate the system of governing ODEs to
obtain the intersection curve segment in the parametric space of each
of
the surfaces. This curve is then further mapped into the 3D model space
to obtain intersection curve segment in the 3D model space.
Issues during Tracing:
The points of the intersection curves are computed successively by
integrating the initial value problem for a system of nonlinear
ordinary differential equations using standard numerical techniques
such as the Runge-Kutta method, Taylor series method or the
Adams-Bashforth method. But when two intersection curves are close to
each other, then step size selection becomes complex and incorrect step
size may lead to a critical problem, straying or looping, which is
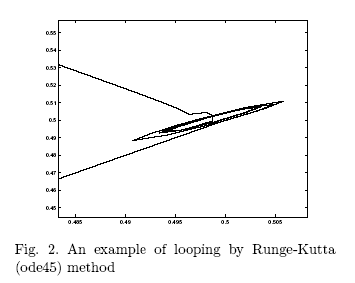
illustrated in Figure 1, 2 and 3. Figure 2 shows the looping phenomenon
when the Runge-Kutta method is used to solve an initial value problem
where we have two intersecting surfaces.

|
|
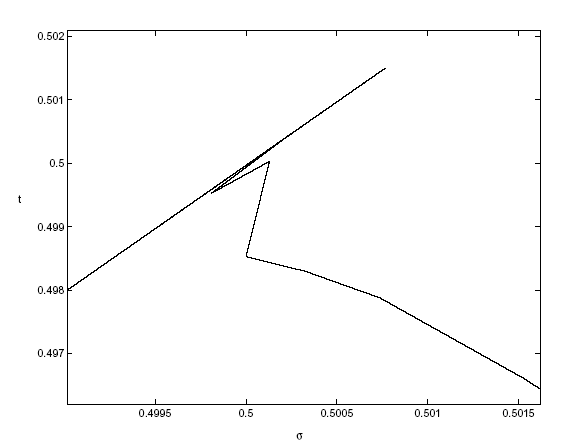
Fig.3. An example of straying in Adams Bashforth method.
|
We list the main issues while tracing.
- Straying or looping.
- Truncation error while integration.
- Error in the initial conditions (caused due to the approximate
solution of a nonlinear
polynomial system of equations).
- Issues of tangential intersection and self-intersections.
Tracing Surface Intersection with Validated Error Bounds:
We specifically are able to solve some of the above problem with the
application of a validated ODE solver. This method we have
devised enables us to obtain validated error bounds for SSI in 3D model
space. The figure given below descibes the flow chart describing the
method.
Last modified on 01-30-2005 by
harishm@mit.edu
Copyright © 2003-2005 Massachusetts Institute of
Technology





