

| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
Research
- The Design Laboratory of the MIT Department of Ocean Engineering was founded in 1972 by Prof. Chryssostomos Chryssostomidis. The laboratory's research has centered on Ship Design, Offshore Structure Design, Marine Robotics , Geometric and Solid Modeling, Advanced Manufacturing, Distributed Information Systems, Computational Geometry, Shipbuilding, Producibility, and Life Cycle issues. Since January 2005, the Design Laboratory has been under Department of Mechanical Engineering.
|
Center for Environmental Sensing and Modeling (CENSAM) 
|
Pervasive sensing provides a new paradigm for monitoring, modeling and control of natural
and infrastructure systems that affect the environment.
CENSAM aims to create a center of excellence in environmental sensing and modeling
that will demonstrate the importance of pervasive sensing through applications
in the well managed urban environment in Singapore.
|
| |||
|
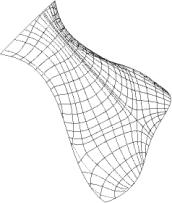
Shape Intrinsic Watermarking (Fingerprinting) |
|
|
The objective of this project is to develop an intrinsic watermark technique
for solids bounded by NURBS surfaces. The key idea is to extract intrinsic
properties of solids, which are not affected by coordinate transformations,
random noise and malicious action of the user. This watermark can be
destroyed only if the digital model describing the shape is changed so
much that the newly represented object cannot any longer be considered
approximately identical to the original solid in the database. |
|
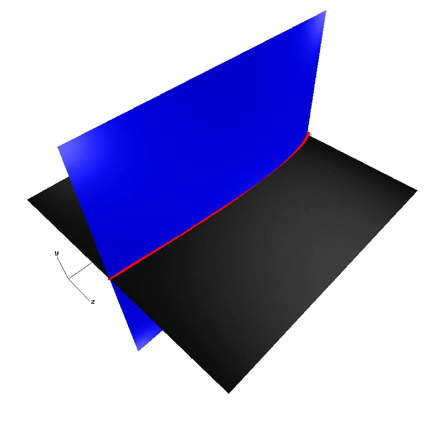
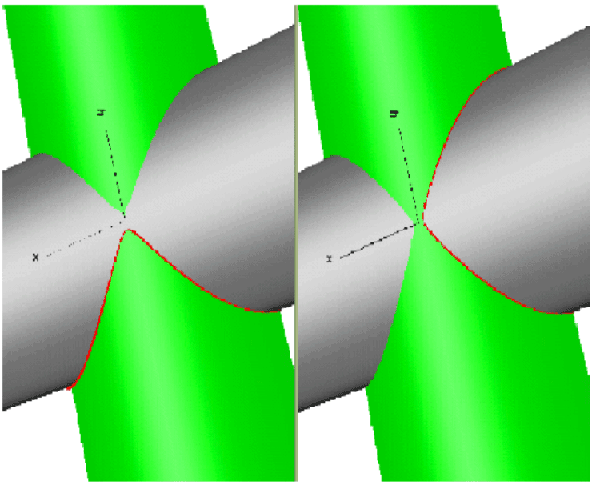
Robust Solid Modeling
|
|

|
Full automation of the design of complex structures requires
reliable geometric computations. This reliability is absent from current
CAD/CAM systems due to their implementation in floating point arithmetic,
which leads to inconsistent and unstable numerical computations. We are
developing a solid modeling system based on interval splines, which differ
from classical splines in that the control point coordinates are represented
as intervals, which in combination with rounded interval arithmetic guarantees
the robustness of geometric computations. A current project involves conversion
of legacy geometric models to robust interval solid models that are topologically
valid and geometrically consistent. Producing rectified models free from
gaps and inappropriate intersections is necessary for effective analysis and
manufacturing. |
|
Representation and Interrogation
Methods for
Functionally Graded Materials |
|


|
With the capability for manufacturing parts
with variable material composition, Solid Freeform Fabrication (SFF) processes
are moving beyond the capabilities of state-of-the-art solid modelers. For
designers to have immediate access to this new technology, methods need
to be developed to facilitate accurate representation, design, and processing
of parts with graded material composition. The four major areas of this
research include the development of a solid modeling method incorporating
graded composition information, composition design tools, processing algorithms
to drive the manufacturing process, and design rules incorporating process
limitations that will be used to evaluate models for manufacturability.
|
|
Rapid Real-Time Interdisciplinary Ocean Forecasting : Adaptive Sampling and Adaptive Modeling in a Distributed Environment |
|
|
Click here to link to the Poseidon project page. |
|
Laser Line Heating |
|

|
Click here to link to the Laser Line Heating Page (Fabrication Laboratory). |
|
Advanced Methods for Inspection |
|

|
Inspection is the process of verifying shape conformance of a measured manufactured part with a toleranced geometric description of a design object. Since milling and casting processes are inaccurate, the need for accurate inspection methods is fundamental, particularly for objects that require a very high level of precision. Inspection is performed by feature extraction, which extracts performance related geometric features from a mathematical design or as--built model; localization, which optimally positions a mathematical design model with respect to a measured manufactured artifact; and local error analysis, which is used for planning remachining operations. A current project involves shape reconstruction of curved objects using interval B-splines. |
|
Praxiteles |
|

|
In order that the design and manufacturing processes
be interactive, algorithms developed in the MIT Design Laboratory for shape
creation, advanced interrogation, visualization, fairing, manufacturing, and
inspection have been integrated into an executive system called Praxiteles.
Praxiteles provides visualization facilities for numerical computations,
and input and output via the IGES format, the standard for geometric data
exchange. Praxiteles facilitates the exchange of curve and surface geometry
between modeling systems through advanced methods for approximate conversions
of high degree Bezier and B-spline surfaces to lower degree representations
with guaranteed bounds on the approximating error. |
|
Developable Surfaces for Shipbuilding |
|
|
Developable surfaces can be manufactured by bending flat plates without stretching or tearing, i.e. by rolling. Their use for ship construction has the advantages of lower labor costs, smaller capital investment, ease of repair and simple tools for construction. We have investigated their design and representation by NURBS surfaces and how to accurately develop them onto a plane. Future projects include the automatic derivation of roller instructions for the fabrication of plates and issues of accuracy control. |
|
|
Formulation of a Model for Ship Transit Risk |
|
|
We have developed
a statistical model for evaluating the relative risk of ship transit through
the nation's ports and waterways. The model is expected to lead to rational
criteria for estimating hydrographic survey priorities. It predicts the
relative risk of physical accidents and, more importantly, the economic
risk of such occurrences in terms of cargo loss and environmental damage.
Projects include the effects of waterway changes (geometry, aids to navigation,
introduction of port management systems, etc.) on ship transit risk. |
|
|
Topologically Reliable Curve and Surface Approximation |
|
|
This project developed piecewise linear approximation methods for the edges and faces of Boundary Representation (B-Rep) solid models. Our method is based on robust geometric definitions and computations, and the existence of a homeomorphism between the exact geometry and its approximation. The approximation consists of an unstructured adaptive triangular mesh. This research has important application for finite element meshing, data exchange, visualization, SFF, and geometric computations. |
|
|
Solution of Nonlinear Systems and Their Applications |
|
|
A fundamental problem in computer aided design is the robust and efficient computation of all real roots of systems of nonlinear polynomial equations. Such problems often occur in computing intersections, distance functions and extrema, and in engineering design. In order to isolate all roots within a given domain our method projects control polyhedra onto a set of coordinate planes and uses rounded interval arithmetic for numerical robustness. Current projects include computing self--intersections of offset curves and surfaces, useful for NC machining, and the rational polynomial representation of pipe surfaces. |
|
|
Mesh Generation |
|
|
This project generates coarse and fine meshes on multiply connected 2D and 3D domains. We have studied the MAT (medial axis transform), which is a point set consisting of points equidistant from two or more points on the boundary contour. Using the MAT, we can extract important shape characteristics and length scales that are used to create a coarse subdivision of a complex surface. Additionally, we can generate fine meshes within individual subregions. This can lead to integration of automated finite element (FE) mesh generation schemes into CAD systems. |
|
|
|
|
| Home | Announcements | Research | People | Sponsors | Courses |
| Publications | Links | Conferences | Help |