13.016 Introduction to Geometric Modeling and Computation

Projection Transformations

OpenGL provides two types of projection transformations: orthographic and perspective. Each of these transformation defines a volume of space called a frustum. Only geometry that is inside of the frusum is displayed on the screen; any portion of geometry that is outside of the frustum is clipped.

• Orthographic

      double left, right, bottom, top, near, far;
      glOrtho(left, right, bottom, top, near, far);
  

  which defines a rectangular parallelpiped frustum.

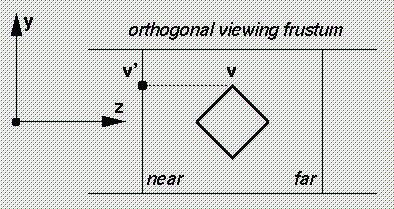
  An orthographic projection projects a 3D point v onto the 2D near clipping plane (sometimes called the picture plane) by constructing a ray through v that is parallel to the viewing direction, i.e. the Z-axis in the eye coordinate system. The (x,y) position on the picture plane where the ray intersects the plane is the 2D projection of v.

  In other words, if v is expressed in the eye coordinate system as (x,y,z), then the orthographic projection is (x,y).

  

• Perspective

      double fov, aspect, near, far;
      gluPerspective(fov, aspect, near, far);
  

  which defines a truncated pyramid frustum.

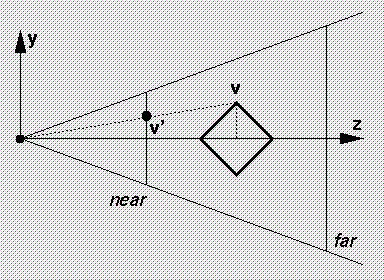
  An perspective projection projects a 3D point v onto the 2D picture plane by constructing a ray through v that passes through the viewpoint direction, i.e. the origin of the eye coordinate system. The (x,y) position on the picture plane where the ray intersects the plane is the 2D projection of v.

  In other words, if v is expressed in the eye coordinate system as (x,y,z), then the perspective projection is (near*x/z, near*y/z).

  

  Note that this function is in the OpenGL utility library, and requires that you include:

      #include <GL/glu.h>
  

Perspective projection produces images that appear more realistic; it more closely mimics the operation of the human eye.

On to specifying the pipeline
Back to projections...
Back to the overview...