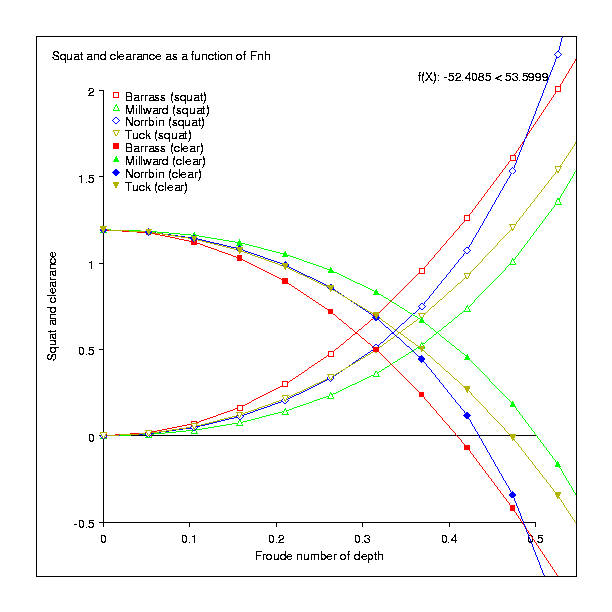
showing that all four models predict the vessel running aground at Froude numbers approximately between 0.4 and 0.5 (indicated by the curves representing clearance intersecting the x-axis).
The following examples are based on vessel traffic and channel configuration characteristics found at the Houston/Galveston Ship Channel:
Channel cross-sectional area Ac = 1189.042886m2; ship immersed cross-sectional area As = 307.218956m2; ship beam B = 32.307224m; ship block coefficient Cb = 0.8; Tuck's form factor Cs = 0.02; channel mean low water depth h = 12.191405m; ship nominal draft T = 11m; and channel mean low water width Wo = 121.914052m.
Setting the ship waterline length L = 236.208476m, the squat and clearance (given in meters) can be calculated for all four squat models as a function of the Froude number of depth Fnh = { 0.1, 0.2, 0.3, 0.4, 0.5 }:
| Froude | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Squat | Clearance | Squat | Clearance | Squat | Clearance | Squat | Clearance | Squat | Clearance |
| Barrass | 0.063376 | 1.128029 | 0.267960 | 0.923445 | 0.622787 | 0.568618 | 1.132953 | 0.058452 | 1.802124 | -0.610719 |
| Millward | 0.028327 | 1.163078 | 0.125742 | 1.065663 | 0.317801 | 0.873604 | 0.644430 | 0.546975 | 1.171691 | 0.019714 |
| Norrbin | 0.043202 | 1.148203 | 0.182177 | 1.009228 | 0.450619 | 0.740786 | 0.930520 | 0.260885 | 1.835103 | -0.643698 |
| Tuck | 0.047480 | 1.143925 | 0.192863 | 0.998542 | 0.445705 | 0.745700 | 0.824719 | 0.366686 | 1.363750 | -0.172345 |
These same results can be displayed graphically:
showing that all four models predict the vessel running aground at
Froude numbers approximately between 0.4 and 0.5 (indicated by the
curves representing clearance intersecting the x-axis).
Ship squat can be plotted as a bivariate function of both Froude number and ship waterline length with 10 contour lines: SQUAT(Fnh, L) = Ci = {0.1, 0.2, ..., 1.0}.
For the Barrass model:
For the Millward model:
For the Norrbin model:
For the Tuck model:
Squat can also be plotted as a trivariate function of Froude number (varying from 0 to 1), ship length (150 to 250m), and ship beam (25 to 40m), SQUAT(Fnh, L, B) = Ci, and displayed interactively as a VRML world (if your web browser is VRML-enabled).
Return to the Ship Squatting Problem home page.
Go to the Ship Squatting Problem evaluation page.
Go to the Ship Squatting Problem univariate plotting
page.
Go to the Ship Squatting Problem bivariate plotting
page.
Go to the Ship Squatting Problem trivariate plotting
page.
This service is a result of the project Formulation of a Model for Ship Transit Risk funded by the U.S. Department of Commerce, U.S. Army Corps of Engineers, and U.S Coast Guard (PIs: N. M. Patrikalakis, MIT, and H. L. Kite-Powell, WHOI).